4.6: Assoziative Regeln

Während beim Kategorisieren die einzelnen Beispiele im Vordergrund der Betrachtung stehen, dienen assoziative Regeln mehr der Beschreibung einer Sammlung bzw. ihrer Eigenschaften. Aber auch sie können als Vorhersage über das Auftreten von Attributwerten aufgefasst werden. Assoziative Regeln können auf binären Attributen folgendermaßen definiert werden.

4.6.1: Assoziative Regel (Klemettinen et al 1994)

In einer Beispielmenge ist eine assoziative Regel also dann zur Basis 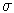erfüllt, wenn der Anteil der Beispiele, bei denen in allen Attributen, die in der Regel genannt sind, eine 1 steht, größer als 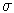ist. Sie ist zum Grad 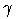erfüllt, wenn der Anteil der Beispiele, bei denen das Attribut B gleich 1 ist, unter denen, bei denen die Attribute aus W gleich 1 sind, größer ist als .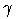

Wie häufig, kann der gleiche Sachverhalt, der hier mit charakteristischen Funktionen definiert wurde, auch mit Mengen definiert werden. Dann spricht man auch vom " Warenkorbmodell". Dazu wird von einer Grundmenge von n "Produkten" ausgegangen. W ist eine Teilmenge, B ein einzelnes Element (Produkt) der Grundmenge und der Beispielmenge entspricht eine Folge von m Teilmengen der Grundmenge. Die Regel W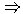B gilt dann zur Basis 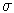, wenn mindestens 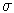m dieser Teilmengen die Menge W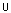{B} enthalten. Sie gilt zum Grad 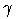, wenn der Quotient aus dieser Anzahl und der Anzahl der Beispielmengen, die W enthalten, größer oder gleich 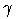ist.

In einer Datenbank über Teilnahme an Lehrveranstaltungen im Fach Informatik könnte z. B. die folgende assoziative Regel gefunden werden:
Einführung in UNIX 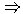Programmieren in C (0.84, 0.34)
Das würde bedeuten, dass 84% der Studierenden, die eine Einführung in UNIX belegt haben auch Programmieren in C belegt haben, und dass insgesamt 34% der Studierenden beide Veranstaltungen belegt haben. Sobald die Anzahl der Attribute größer wird, kann es sehr viele solche assoziativen Regeln geben, auch wenn der Grad groß gewählt wird. Zu ihrer Bestimmung werden eine ganze Reihe von Methoden und Verfahren entwickelt, auf die hier aber nicht näher eingegangen werden soll.

Abb. 65: Anzahl der Regeln aus zwei Beispielsammlungen

In Abbildung _65_ sind zwei Beispiele aus Klemettinen et al. ( [->]1994) angegeben. In beiden Fällen ist die Anzahl der Regeln hoch. Bei den Beispielen aus dem Computerversand ist sie allerdings noch erheblich größer als bei den Belegungen von Lehrveranstaltungen. Das kann zum einen dadurch erklärt werden, dass die Rechner eher in standardisierten Zusammenstellungen geliefert werden, zum anderen aber auch dadurch, dass die Anzahl der Attribute größer und die Anzahl der Beispiele kleiner ist. Bei der Basis 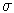=0.06 und 524 Beispielen kann eine Regel gefunden werden, wenn mehr als 31 Beispiele die Bedingungen der linken Seite erfüllen. Zudem ist die mittlere Anzahl von belegten Attributen im zweiten Beispiel höher.

In beiden Fällen ist die Anzahl der Regeln zu groß, um sie noch sinnvoll "von Hand" sichten und auswerten zu können. Es müssen daher automatisierte Verfahren verwendet werden, um interessante Teilmengen zu finden. Zudem gibt es Regeln, die sich bereits aus der Natur der Daten ergeben und daher nicht weiter interessant sind. So ist die Regel
Design and Analysis of Algorithms Fundamentals of ADP (0.97, 0.03)
die besagt, dass 97% der Studierenden, die den Kurs "Design and Analysis of Algorithms" belegt haben, im Laufe ihres Studiums auch den Kurs "Fundamentals of Automated Data Processing" belegt hatten, nicht sonderlich erstaunlich, wenn der zweite Kurs ein Einführungskurs ist, den die meisten Studierenden zu Beginn ihres Studiums belegen.

Um trotz der großen Zahl möglicher Regeln Wissen zu extrahieren teilen Klemettinen et al. ( [->]1994) die Kurse in Teilmengen wie z. B. "basic courses" und "graduate courses" oder Kurse verschiedener Fachgebiete ein. Dadruch wird Wissen über das Themengebiet eingebracht, das genutzt werden kann um Regeln zu formulieren. Mit Hilfe der Einteilungen können Kurse spezifiziert und ausgewählt werden. Dazu verwenden Klemettinen et al. sogenannte Templates.

4.6.2: Template

Mit Hilfe dieser Templates können nun Mengen von Regeln bestimmt werden. Dazu kann zunächst ein positives Template angegeben werden. Das System zeigt dann alle Regeln, die von diesem Template erfasst werden, an. Zusätzlich kann ein negatives Template angegeben werden. Die Regeln, die von diesem Template erfaßt werden, werden dann wieder von der Anzeige ausgeschlossen. Dieses Verfahren ist damit quasi ein Suchverfahren auf der Menge der assoziativen Regeln: die Teilmengen W_j geben Bedingungen an, mit denen eine Teilmenge der Regeln bestimmt wird.

Dieses Verfahren wurde für binäre Attribute entwickelt, also für den Fall, in dem Mengen durch ihre charakteristische Funktion dargestellt werden. Deshalb müssen zur Verallgemeinerung Teilmengen der Menge der Attribute verwendet werden.

Bei nichtbinären Attributen kann man Verallgemeinerungen dadurch beschreiben, dass man Teilmengen der Wertemenge eines Attributs als Attributwerte zulässt, in der Sprache des AQ Algorithmus also auch Selektoren als Attributwerte erlaubt. Diese Teilmengen des Wertebereichs können z. B. durch eine streng hierarchische Klassifikation beschrieben werden. Auch hier wird durch die Klassifikation Wissen über das Themengebiet eingebracht, das benutzt werden kann, um Regeln zu formulieren. So könnte man die Lebensjahre eines Menschen in Kindheit, Jugend, Berufsfähigkeit und Rentenalter einteilen. Das dritte Lebensjahr ist z. B. ein Teil der Kindheit, oder umgekehrt die Kindheit eine Verallgemeinerung des dritten Lebensjahres. Existenzaussagen, die über ein Beispiel mit dem spezifischeren Wert gelten, gelten dann auch für den verallgemeinerten Wert: Aus der Aussage "Karl ist drei Jahre alt" ( 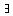x: mit alter(x)=3Jahre und name(x)=Karl ) kann man folgern: "Karl ist ein Kind" ( 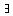x: mit alter(x)Kindheit und name(x)=Karl )

Man kann die Ordnung des Wertebereichs, die durch ein hierarchisches Klassifikationssystem gegeben ist, auch anders beschreiben: Lässt man die Namen der Klassen (also z. B. Kindheit, Jugend) als Werte des Attributs zu, difiniert die Teilmengenrelation eine Teilordnung auf diesem erweiterten Wertebereich.

4.6.3: Teilordnung

Auf einer Menge kann es mehrere Teilordnungen geben.

Um aus einem hierarchischen Klassifikationssystem auf einer Menge R eine Teilordnung abzuleiten, verwendet man die Mengeninklusion auf der Potenzmenge P(R) , also der Menge aller Teilmengen von R . Für diese Teilordnungen ist die Menge R ein maximales Element. Geht man zum System der in der Klassifikation vorkommenden Teilmengen über, bleibt die Teilordnung mit maximalem Element erhalten. Weil durch die Teilmengen streng hierarchischen Klassifikation eines Themengebiets Konzepte definiert werden bezeichnet man die so erzeugte Teilordnung auch als Konzepthierarchie.

Ein KDD-Verfahren, das mit solchen Teilordnungen arbeitet, soll im folgenden vorgestellt werden.

4.6.4: DBlearn / DBMiner