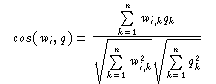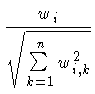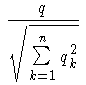3.4.6.2: Das
Cosinusmaß
Ein solches Maß ist das Cosinusmaß (der
Cosinus im Rn ):
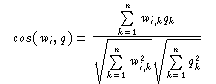
Wie der Cosinus in der Ebene
liegen die
Ähnlichkeitswerte
zwischen zwei Vektoren immer im Intervall
[-1,1] . Die beiden Wurzeln im Nenner sind
gerade die euklidischen Längen der Vektoren wi und q . Man kann sich die Formel also auch als einfaches
Skalarprodukt der normierten Vektoren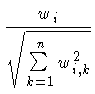
und 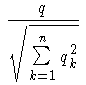
vorstellen.
Das ist auch der Grund für die Wahl des Maßes:
Die Ähnlichkeitswerte sind in gewissem Sinne unabhängig von
der euklidischen Länge der Vektoren, also der Anzahl und
Größe der von 0 verschiedenen Einträge. Sie
hängen lediglich von der "Richtung" der
Vektoren ab, also dem Verhältnis der Vektoreinträge
untereinander. Werden nun zwei Vektoren mit dem
Cosinusmaß verglichen, so ist ihre Ähnlichkeit
am
größten, wenn sie die gleiche Richtung haben, unabhängig
von ihrer Länge, d. h. wenn sie sich nur durch einen
positiven Faktor voneinander unterscheiden.
Die Vektoren mit gleicher
Ähnlichkeit zu einem Referenzvektor sind also
die, die den selben Winkel mit dem Referenzvektor bilden.
Im zweidimensionalen sind das zwei Strahlen, die
symmetrisch zum Referenzvektor von (0,0) ausgehen.
© 1999 / HTML-Version 13. 7. 1999: R. Ferber, email: R. Ferber