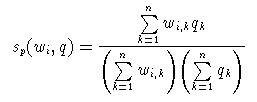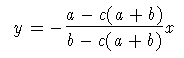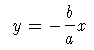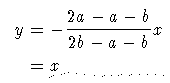3.4.6.3: Das
Pseudo-Cosinusmaß
Beim Pseudo-Cosinusmaß sind
die euklidischen Längen
durch die Summe der
Vektoreinträge (die L1 Länge) ersetzt.
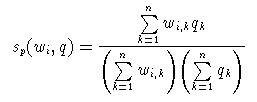
In diesem Sinne kann auch dieses Maß als
Skalarprodukt ( L1 - ) normierter Vektoren aufgefasst werden.
Solange die Vektoreinträge bzw. Gewichte wi,j und qi alle positiv sind, reagiert diese Normierung vor
allem weniger stark auf große Werte unter den Einträgen, d.
h. diese werden weniger stark
abgeschwächt.Die Vektoren mit
gleicher Ähnlichkeit zu einem Referenzvektor
sind hier auch radiale Strahlen aus dem
Nullpunkt, allerdings nicht mehr durch den Winkel
charakterisiert. Im zweidimensionalen Fall ergibt sich
folgendes: Sei wieder (a,b) der Referenzvektor, zu dem der Vektor
(x,y) die Ähnlichkeit c habe, dann gilt:
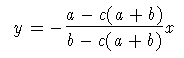
Für den Fall
c=1 folgt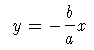
Für c=0.5 folgt 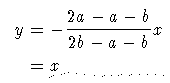
Für c->∞ geht die Steigung der Geraden gegen -1 . Das Verhalten ist also nicht symmetrisch zum
Referenzvektor wie beim Cosinus.
Mit wachsendem c wandert der Strahl mit den Vektoren mit
Abstand c zunächst in Richtung auf die
Achse, die den kleineren Winkel zum Referenzvektor hat,
um schließlich gegen die Gerade y=-x zu konvergieren. Lässt man nur positive Einträge in den
Vektoren zu, liegen die Ähnlichkeitswerte zwischen
0 und 1 ; die Ähnlichkeit ist für einen Vektor am
größten, der genau in die Richtung der Achse der
größten Komponente des Referenzvektors zeigt, also nur
für diese Komponente einen Eintrag ungleich 0 besitzt. Ein solches Verhalten ist im
Allgemeinen nicht wünschenswert.
© 1999 / HTML-Version 13. 7. 1999: R. Ferber, email: R. Ferber