R. Ferber: Informationssysteme 1.5.4.3.13

4.4.2.3: Häufigkeit der Terme

Im Abschnitt _3.4.3_ über Gewichtungsmethoden und beim probabilistischen Retrieval waren IDF-Maße eingeführt worden, die seltenen Termen höhere Gewichte zuordnen. Diese Gewichtung wurde vorgenommen, weil seltenen Termen eine höhere Diskriminationsfähigkeit zugeschrieben wird (vergleiche Abbildung _32_ ). Peat und Willett (1991 [->]) führen die Mißerfolge der automatischen Expansion darauf zurück, dass dabei häufige und damit wenig nützliche Terme gefunden werden. Sie haben diesen Effekt für drei Maße, das Cosinusmaß

das Dice-Maß

und das Jaccard-Maß (hier Tanimoto-Maß enannt)

untersucht. Dabei bezeichnet H(X) die Anzahl der Dokumente, in denen der Term X auftritt, und H(X,Y) die Anzahl der Dokumente, in denen die Terme X und Y zusammen vorkommen. (Die Maße werden hier mit Dokumenthäufigkeiten formuliert. Setzt man in den Formeln aus Abschnitt _3.4.6_ charakteristische Funktionen (also Vektoren mit den Einträgen 0 und 1) ein, gehen z. B. die Summen der Quadrate im Nenner des Cosinusmaßes in solche Häufigkeiten über.)

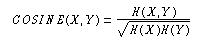
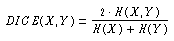
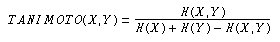
Betrachtet man die Formeln aus statistischer Sicht, zeigt sich allerdings, dass sie häufige Terme begünstigen: Während die angegebenen Maße Ähnlichkeiten oder Winkel zwischen Vektoren messen, kann man auch überlegen, ob die Häufigkeit, mit der zwei Terme zusammen auftreten, zufällig, überzufällig oder unterzufällig ist.

Falls p(X) die Wahrscheinlichkeit des Auftretens des Terms X in einem Dokument und p(XY) die Wahrscheinlichkeit des gemeinsamen Auftretens der Terme X und Y in einem Dokument bezeichnen, gilt nach der Definition der statistischen Unabhängigkeit bei zufälligem gemeinsamen Auftreten der Terme

p(XY)=p(X)·p(Y)

Der Quotient

ist also genau dann kleiner als 1 , wenn die Terme unterzufällig häufig zusammen auftreten, er ist gleich 1 , wenn sie zufällig häufig zusammen auftreten, und er ist größer als 1 , wenn sie überzufällig häufig zusammen auftreten.

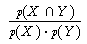
Ersetzt man die Wahrscheinlichkeiten durch relative Häufigkeiten, erhält man die Formel

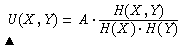
wobei A die Anzahl der Dokumente bezeichnet, die bei der Berechnung der relativen Häufigkeit herangezogen wurden, und als konstanter Faktor in den folgenden Überlegungen ignoriert werden kann.

Vergleicht man diesen Quotienten mit den Ähnlichkeitsmaßen, so zeigt sich, dass alle drei Maße häufige Terme stärker begünstigen als dieser. Der COSINE(X,Y) z. B. unterscheidet sich von U(X,Y) durch den Faktor

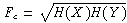
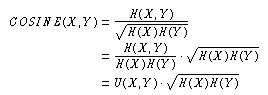
Je häufiger ein Term ist, desto größer ist also der Faktor F_c .

Für die beiden anderen Maße lassen sich ähnliche Effekte zeigen:

Um einen Faktor F_D für das Dice - Maß zu berechnen setzen wir

f·DICE(X,Y)=U(X,Y)

mit fR . Dann folgt

Mit F_D=⁽¹⁾/_(f) erhalten wir schließlich

DICE(X,Y)=F_D·U(X,Y)

Auch dieser Faktor F_D wächst mit zunehmender Häufigkeit der Terme X und Y .

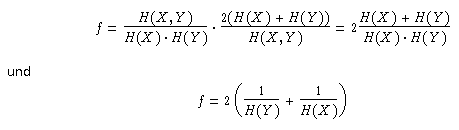
Für das Tanimoto-Maß schließlich führt

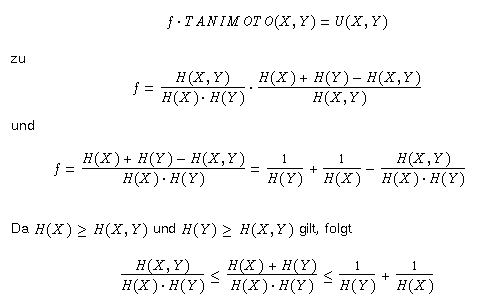
Wobei f=g gilt, wenn H(X,Y)=0 gilt. Schließlich können wir F_T=⁽¹⁾/_(g) setzen und erhalten

TANIMOTO(X,Y)=⁽¹⁾/_(f)·U(X,Y)>=F_T·U(X,Y)

Auch der Faktor F_T kann also mit zunehmender Häufigkeit der beteiligten Terme wachsen und damit häufige Terme begünstigen.