Diese Seiten sind urheberrechtlich geschützt. Die Verantwortung für
die Inhalte und die Rechte der Online-Version liegen beim Autor
Reginald Ferber, Münster (Westf).
Die Rechte der gedruckten Version
beim dpunkt.verlag, Heidelberg. Die Weiterverwendung von Texten oder
Abbildungen - auch auszugsweise - ist ohne die schriftliche Zustimmung des Autors
Reginald Ferber
bzw. des dpunkt.verlags nicht gestattet.
Es wird darauf hingewiesen, dass die verwendeten Soft- und Hardware-Bezeichnungen sowie Markennamen und Produktbezeichnungen
der jeweiligen Firmen im Allgemeinen warenzeichen-, marken-, oder patentrechtlichem Schutz unterliegen.
Alle Angaben und Programme wurden mit großer Sorgfalt kontrolliert. Trotzdem kann keinerlei Haftung
für Schäden irgendwelcher Art übernommen werden, die sich im Zusammenhang mit der Nutzung dieser Seiten
ergeben.
Diese HTML-Datei wurde am 27-10-2003 erzeugt.

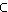 G
Ereignisse eines
Wahrscheinlichkeitsraums mit der
Wahrscheinlichkeitsfunktion
p
. Dann heißt der
Ausdruck
G
Ereignisse eines
Wahrscheinlichkeitsraums mit der
Wahrscheinlichkeitsfunktion
p
. Dann heißt der
Ausdruck
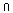 Y)=p(
X)·p(Y)
Y)=p(
X)·p(Y)
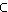 R1
und
X2
R1
und
X2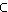 R2
gilt
R2
gilt
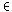 X1
)
X1
)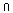 (A2
(A2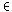 X
2))=p(
(A1
X
2))=p(
(A1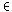 X1)
)·p((A
2
X1)
)·p((A
2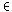 X2))
X2))
