2.3.9.2: Koeffizientenbestimmung
Auch bei der Bestimmung der Koeffizienten kann man
wieder verschiedene Verfahren und Gütefunktionen
verwenden. Für die binäre Entscheidung mit einer LTU
verwendeten Brodley und Utgoff das klassische Verfahren der
(rekursiven) Methode der kleinsten
Fehlerquadrate (Recursive Least
Squares,
RLS).
Ziel ist es dabei, die Summe
|
 |
d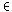 T T |
|
(d·x-zd)2 |
der Quadrate der Abweichungen des Skalarprodukts für das Beispiel
d
von dem vorgegebenen Entscheidungswert
zd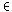 {-1,1}
zu minimieren.
Dazu werden Methoden aus der linearen Algebra
verwendet. Zu dem Koeffizientenvektor
x
einer linearen Schwellwertfunktion wird für
jedes Beispiel
d=(w0,...,wn)
der Vektor {-1,1}
zu minimieren.
Dazu werden Methoden aus der linearen Algebra
verwendet. Zu dem Koeffizientenvektor
x
einer linearen Schwellwertfunktion wird für
jedes Beispiel
d=(w0,...,wn)
der Vektor
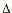 x=-Pjd(d·x-zd
) x=-Pjd(d·x-zd
)
|
addiert.
Pj
bezeichnet
dabei die Fehlerkovarianzmatrix, die nach jedem Schritt
neu berechnet wird (siehe Brodley und Utgoff, 1995 [->]
) und den Einfluss
der Veränderungen kleiner werden lässt. Die RLS
ist verhältnismäßig aufwändig, garantiert aber bei
linear separierbaren Beispielen ein richtiges Ergebnis (wenn auch
eventuell erst nach mehreren Durchgängen).
Es gibt auch
einfachere Methoden, die Koeffizientenvektoren
einer linearen Schwellwertfunktion oder einer linearen
Maschine zu ändern. Um zu erreichen, dass
ein bisher falsch klassifiziertes Beispiel in einer
binären linearen Maschine richtig klassifiziert
wird, kann man zu dem
Koeffizientenvektor x
der Menge, in die das Beispiel
gehört, ein skalares Vielfaches des Beispielvektors d
addieren und von dem Koeffizientenvektor y
der Menge,
der es fälschlich zugewiesen wurde,
denselben Korrekturvektor abziehen. Den skalaren Faktor kann man aus der Beziehung
(x+cd)*d-(y-cd)
*d=0
folgendermaßen herleiten:
(x+cd)*d-(y-cd)
*d=(x-y)*d+2cd*d
und damit
| c=- |
| (x-y)*d |
 |
|
2d*d |
|
Weiter kann man eine kleine positive Zahl
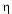 zu dem Faktor hinzuaddieren. Dadurch liegt das
Beispiel nicht genau auf der Grenze der beiden Entscheidungsmengen.
zu dem Faktor hinzuaddieren. Dadurch liegt das
Beispiel nicht genau auf der Grenze der beiden Entscheidungsmengen.
Man kann nun sequenziell die Beispiele durchgehen und
immer dann, wenn ein Beispiel von der aktuellen Entscheidungsfunktion
falsch zugeordnet wird, diese so ändern, dass es richtig zugeordnet
wird. Wenn die Mengen der Beispiele aber nicht linear separabel sind,
kann dieses Verfahren nicht konvergieren. Man kann
aber versuchen, den Einfluss von einigen
wenigen Ausreißern zu verringern. Dazu
kann man den skalaren
Faktor mit einer zeitlichen Dämpfung
versehen, sodass die
Korrekturen im Laufe des Algorithmus immer geringer
werden.
Ein anderes Verfahren wird im
Pocket-Algorithmus von Gallant
verwendet: Hier werden zunächst alle Koeffizienten auf 0
gesetzt. Mit dieser Entscheidungsfunktion werden dann so lange zufällig
ausgewählte Beispiele der Trainingsmenge klassifiziert, bis ein Beispiel
falsch klassifiziert wird. Die Anzahl der bis dahin richtig klassifizierten Beispiele wird
zusammen mit den Koeffizientenvektoren in der "Pocket"
P
gespeichert und ein Lernschritt ausgeführt,
sodass das fehlerhafte Beispiel richtig klassifiziert wird.
Dann werden mit dieser neuen Entscheidungsfunktion wieder zufällig ausgewählte
Beispiele klassifiziert, bis ein Fehler auftritt. Ist die Anzahl der so richtig klassifizierten
Beispiele größer als die der Funktion, die in
P
gespeichert ist, wird diese
durch die aktuelle Funktion ersetzt. Durch die zufällige Auswahl
der Beispiele soll so in einem Hill-Climbing-Prozess eine möglichst gute
Entscheidungsfunktion ermittelt werden.
|

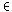 {-1,1}
zu minimieren.
Dazu werden Methoden aus der linearen Algebra
verwendet. Zu dem Koeffizientenvektor
x
einer linearen Schwellwertfunktion wird für
jedes Beispiel
d=(w0,...,wn)
der Vektor
{-1,1}
zu minimieren.
Dazu werden Methoden aus der linearen Algebra
verwendet. Zu dem Koeffizientenvektor
x
einer linearen Schwellwertfunktion wird für
jedes Beispiel
d=(w0,...,wn)
der Vektor
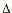 x=-Pjd(d·x-zd
)
x=-Pjd(d·x-zd
)
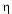 zu dem Faktor hinzuaddieren. Dadurch liegt das
Beispiel nicht genau auf der Grenze der beiden Entscheidungsmengen.
zu dem Faktor hinzuaddieren. Dadurch liegt das
Beispiel nicht genau auf der Grenze der beiden Entscheidungsmengen.

