3.4.3: Ein Spreading-Activation-Modell

An zweiter Stelle in der Bewertung der automatischen Retrieval-Verfahren in TREC-4 liegt das System PIRCS (Kwok, Grundfeld und Lewis, 1995 [->] ; Kwok und Grunfeld, 1996 [->] ), das am Queens College der City University of New York entwickelt wurde. Es handelt sich dabei auch um ein probabilistisches System, das mit Termen und Termpaaren indexiert und auf Teildokumenten arbeitet. Es verwendet wie viele andere Systeme Pseudo-Relevance-Feedback, nutzt also die in einem ersten Lauf am besten bewerteten (Teil-)Dokumente, um die Anfrage in einem zweiten Lauf um weitere Terme zu ergänzen. Es wird von den Autoren in ihrem Beitrag zu TREC-3 als ein "Spreading-Activation-Modell" vorgestellt. Ähnlich wie INQUERY besteht das Modell aus einem Netz mit drei Schichten mit Knoten, die die Anfragen, die Terme und die Dokumente repräsentieren (siehe Abbildung 86 ). Es bestehen gewichtete Verbindungen zwischen den "benachbarten" Schichten, d.h. zwischen der Anfrageschicht und der Termschicht und zwischen der Termschicht und der Dokumentschicht.

Abbildung 86: Das Netz des PIRCS-Systems

Wird ein Knoten des Netzes aktiviert, wird diese Aktivität in einem Aktivierungszyklus auf die Knoten übertragen, zu denen eine Verbindung besteht. Dabei wird sie mit dem Gewicht multipliziert, das der Verbindung zugeordnet ist. Aus den in einem Knoten eintreffenden Aktivierungswerten wird dort durch eine "lokale Funktion" ein neuer Aktivierungswert berechnet. Die einfachste (und auch am häufigsten verwendete) lokale Funktion ist das Aufsummieren der eintreffenden Werte. In dem Beitrag zu TREC-4 wird die Ähnlichkeitsfunktion des Systems als eine Kombination von zwei Ähnlichkeitsmaßen dargestellt, wobei der Zusammenhang mit der Netzdarstellung nicht sonderlich klar wird. Dazu werden für jede Anfrage q zwei Anfragevektoren v_q=(v_q,1,...,v_q,n ) und w_q=(w_q,1,...,w_q,n ) eingeführt. Analog werden für jedes Dokument d_i zwei Dokumentvektoren w_i=(w_i,1,...,w_i,n ) und v_i=(v_i,1,...,v_i,n ) definiert. Als Ähnlichkeit zwischen dem Dokument und dem Vektor wird die Funktion

s(di,q) =c(wi·vq) +(1-c) (vi·wq)

verwendet, wobei c ein Parameter zwischen 0 und 1 ist. Aus dem TREC-4-Beitrag lassen sich die folgenden Gewichtsformeln zur Berechnung der Anfrage- und Dokumentvektoren ableiten, wobei die Darstellung mal wieder nicht sehr klar ist.

wi,k=ln (

N-h(k) h(k)

)·f

(q,k)

vi,k=S (

h(i,k) l(di)

)

Dabei bezeichnet N die Anzahl von Termen in allen Dokumenten, h(k) die Häufigkeit des Terms k in allen Dokumenten (also gilt

N=

n 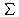k=1

h

(k )

), h(i,k) die Häufigkeit des Term k im Dokument d_i und l(d_i) die Länge des Dokuments d_i . Für Anfragen werden die Werte analog berechnet. f(q,k) ist ein "Lernfaktor", der zunächst gleich 1 gesetzt wird, zum Relevance Feedback aber den Wert

f

(q,k)

=ln

h(q,k) l( q)-h(q,k)

annehmen kann. S wird lediglich als "signal function to suppress outlying values" eingeführt.

Betrachtet man die Gewichtsformeln genauer, so zeigt sich, dass in w_i,k bis auf den Lernfaktor nur globale Einflussfaktoren vorkommen, in v_i,k nur lokale. Für f(q,k)=1 gilt also für beliebige Anfragen q und beliebige Dokumente d_i w_i,k=w_q,k . Damit kann man die Ähnlichkeitsfunktion in diesem Fall also auch folgendermaßen schreiben:

s(di,q)

= c(wi·vq) +(1-c) (vi ·wq)

=

n 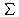k=1

(c(wi,kvq,k)+(1-c)vi,kwq,k)

=

n 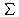k=1

wi,k(c(vq,k)+(1-c)vi,k)

=

wi· (cvq+(1-c)vi)

=

n 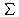k=1

( ln

N-h(k) h(k)

( c·S (

h(q,k) l(q)

) +(1-c) S (

h(i,k) l(i)

) ) )

Damit entpuppt sie sich (im Fall f(q,k)=1 ) entweder als Skalarprodukt zwischen einem Dokumentvektor, der nur globale Einflussfaktoren berücksichtigt, und einer Linearkombination aus einem Dokumentvektor und einem Anfragevektor oder aber - was sinnvoller erscheint - als eben diese Linearkombination, wobei die globalen Termeigenschaften als Faktoren aufmultipliziert werden. Es scheint aber so zu sein, dass in der Summe nur über die Terme summiert wird, die in der Anfrage auftauchen. Dadurch wird quasi eine boolesche Anfrage vorgeschaltet.

Zur Berechnung der Ergebnislisten wurden die Wörter der Anfragen zunächst auf Wortstämme reduziert und eine Stoppwortliste verwendet. Damit ergaben sich Anfragen mit im Mittel 6,22 Termen. Die Dokumente wurden in Teildokumente von je ca. 550 Wörtern zerlegt. Aus diesen Dokumenten wurden 642 755 verschiedene Terme isoliert. Weiter wurden halbautomatisch 55 599 Termpaare ermittelt.

Aus den Teildokumenten wurden mit dem oben beschriebenen Verfahren die 40 besten Teildokumente für die Expansion ermittelt und zum Relevance Feedback verwendet. Aus diesen Teildokumenten wurden die 50 besten Terme herausgesucht. Dabei wurden nur Terme, die fünfmal oder häufiger auftraten, berücksichtigt. Die Auswahl basierte auf der mittleren Auftretenswahrscheinlichkeit in den 40 Teildokumenten. Die 50 Terme wurden zu den ursprünglichen Anfragetermen hinzugefügt. Mit diesen erweiterten Anfragen wurden dann die endgültigen Resultatlisten erstellt.

Über diese automatisch erstellten Ergebnislisten hinaus wurden noch manuell erweiterte Anfragen erzeugt. Dazu konnten zum einen die Terme durch Wiederholen höher gewichtet werden, zum anderen konnten neue Terme hinzugefügt werden. In dieser Kategorie war PIRCS ebenfalls Zweitbester.

Abbildung 87: Ergebnisse der PIRCS-Verfahren in TREC-4

Abbildung 88: Vergleich der PIRCS-Verfahren mit anderen TREC-4-Systemen