3.4.5: Das Okapi-System
Im Okapi-System der City University of
London (Robertson, Walker, Hancock-Beaulieu und Gatford, 1995 [->]
;
Robertson, Walker, Beaulieu, Gatford und Payne, 1996 [->]
)
wurde die Robertson-Sparck-Jones-Formel
(siehe Abschnitt 3.2.3
) verwendet.
Es unterscheidet sich daher von anderen
Vektorraummodellen dadurch, dass Gewichte für Terme
in Abhängigkeit von einer Anfrage berechnet
werden:
| vk=ln |
| (R(
q,k)+0,5)/(
R(q)-R(q,k)
+0,5) |
 |
| (d(
k)-R(q,k)
+0,5)/(N-d(k)
-R(q)+R(q,k)
+0,5) |
|
wobei
N
die Anzahl der Dokumente in der Sammlung bezeichnet,
R(q)
die Anzahl der zur Anfrage
q
relevanten Dokumente in der Trainingsmenge,
d(k)
die Anzahl der Dokumente, die den Term
tk
enthalten, und
R(q,k)
die Anzahl der relevanten Dokumente, die den Term
tk
enthalten. In das Ähnlichkeitsmaß zwischen einem
Dokumentvektor
wi
und einem Query-Vektor
q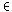 {0,1}n
gehen die Gewichte
über das Skalarprodukt {0,1}n
gehen die Gewichte
über das Skalarprodukt
| s |
(wi,q) |
= |
|
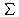 |
| {j | qj=1} |
|
wi,j= |
| n |
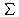 |
| j=1 |
|
wi,j·qj= |
| n |
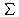 |
| j=1 |
|
h |
(i,j) |
·v
j·qj |
ein, wobei
wi,j=vj·h(i,j)
gesetzt wird
und
h(i,j)
wieder die Häufigkeit
des Terms
tj
im Dokument
di
bezeichnet.
Mit der Verwendung von Relevanzdaten und termstatistischen Daten
für die Gewichte unterscheidet sich das Vorgehen bei Okapi z.B.
von der in INQUERY gewählten Methode, bei der die Berechnung der
Gewichte von der spezifischen Anfrage unabhängig ist. Man kann den
Okapi-Ansatz aber auch als Berechnung eines Anfragenetzes, wie es im
Allgemeinen Modell eines bayesschen Netzwerks beschrieben ist,
auffassen.
Die Robertson-Sparck-Jones-Formel bildet nur
das Herzstück der in TREC-4 tatsächlich verwendeten
Gewichts- bzw. Ähnlichkeitsformel.
In sie gehen auch die Häufigkeiten des Terms in Dokument und Anfrage und diverse
andere Parameter der Dokumentensammlung ein (z.B.
die mittlere Dokumentlänge). Weitere Parameter der Formel können
für die jeweilige Sammlung optimiert werden.
Die Testdaten in TREC enthalten für die Ad-hoc-Aufgabe neue Anfragen.
Das heißt, aus den Trainingsdaten lassen sich für
die Robertson-Sparck-Jones-Formel keine Werte
für
R(q)
und
R(q,k)
gewinnen. Sie wurden
- wie bei den anderen Systemen -
aus den besten Dokumenten nach einem ersten Anfragedurchgang ermittelt.
Dazu wurden Terme, die nicht in der Ausgangsanfrage vorkamen,
mit der Robertson-Sparck-Jones-Formel gemäß der
tatsächlichen Häufigkeiten gewichtet. Die
Terme der Ausgangsanfrage wurden
stets so gewichtet, als ob sie in 19 von 20 Dokumenten
aufgetreten wären.
Für das automatische Retrieval in TREC-4 wurde
als Retrieval-Wert eines Dokuments eine
Kombination aus dem Retrieval-Wert des ganzen Dokuments und
dem Retrieval-Wert der besten Passage
berechnet. Eine Passage wurde
dabei als Folge von Absätzen
definiert, wobei eine Minimal- und eine Maximalzahl von
Absätzen festgelegt wurde. Die verwendeten Grenzwerte
waren 1 und 20
bzw. 4 und 32.
Offenbar wurden dabei lediglich Passagen am Beginn und
Ende eines Dokuments berücksichtigt. Die Ergebnisse
sind in Abbildung 90
dargestellt.
|

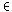 {0,1}n
gehen die Gewichte
über das Skalarprodukt
{0,1}n
gehen die Gewichte
über das Skalarprodukt
 Abbildung 90: Ergebnisse mit Okapi in TREC-4
Abbildung 90: Ergebnisse mit Okapi in TREC-4