4.2.1.2: Beispiel: Würfel
Um das Werfen eines Würfels durch einen
Wahrscheinlichkeitsraum zu beschreiben kann man als
Grundraum die
Menge G={1,...,6} der Augenzahlen eines
Wurfes betrachten.
Ein Würfel ist fair, wenn jedes elementare Ereignis,
also das Fallen einer Zahl, die
Wahrscheinlichkeit p({x})=(1)/(6) hat. Das Ereignis X={1,3,5} G ist dadurch definiert,
dass eine der Augenzahlen der Teilmenge
gewürfelt wird, d. h. dass
eine ungerade Zahl
fällt. Die
Wahrscheinlichkeit des Ereignisses ergibt
sich aus p(X)=p({1,3,5})=p({1}
G ist dadurch definiert,
dass eine der Augenzahlen der Teilmenge
gewürfelt wird, d. h. dass
eine ungerade Zahl
fällt. Die
Wahrscheinlichkeit des Ereignisses ergibt
sich aus p(X)=p({1,3,5})=p({1}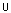 {3}
{3}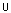 {5})=p({1})+p({3})+p({5})=(3)/(6)=(1)/(2)
{5})=p({1})+p({3})+p({5})=(3)/(6)=(1)/(2)
© 1999 / HTML-Version 13. 7. 1999: R. Ferber, email: R. Ferber








 G ist dadurch definiert,
dass eine der Augenzahlen der Teilmenge
gewürfelt wird, d. h. dass
eine ungerade Zahl
fällt. Die
Wahrscheinlichkeit des Ereignisses ergibt
sich aus p(X)=p({1,3,5})=p({1}
G ist dadurch definiert,
dass eine der Augenzahlen der Teilmenge
gewürfelt wird, d. h. dass
eine ungerade Zahl
fällt. Die
Wahrscheinlichkeit des Ereignisses ergibt
sich aus p(X)=p({1,3,5})=p({1}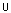 {3}
{3}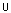 {5})=p({1})+p({3})+p({5})=(3)/(6)=(1)/(2)
{5})=p({1})+p({3})+p({5})=(3)/(6)=(1)/(2) 


