4.2.1: Wahrscheinlichkeitsrechnung in endlichen Mengen

Bevor das Modell vorgestellt wird, sollen zunächst ein paar Begriffe aus der Wahrscheinlichkeitsrechnung endlicher Wahrscheinlichkeitsräume in Erinnerung gerufen werden.

4.2.1.1: Endlicher Wahrscheinlichkeitsraum

Aus der Definition folgt unmittelbar

p(Ø)=0

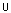1=p(G)=p(GØ)=p(G)+p(Ø)=1+p(Ø)

4.2.1.2: Beispiel: Würfel

Man sieht unmittelbar, dass sich dieser Sachverhalt auch mit Attributen und Bedingungen schreiben lässt: Als Attribut A₁:G->G wählt man die Augenzahl eines Würfelwurfs. Dann ist X=(A₁{1,3,5}) die Menge der Würfe mit ungerader Augenzahl. Die Wahrscheinlichkeit kann dann auch so geschrieben werden: p(X)=p((A₁{1,3,5}))=⁽¹⁾/₍₂₎ . Das Attribut A₁ wird dann auch als Zufallsvariable bezeichnet, und in der Formel wird die innere Klammer häufig weggelassen.

Würde man nicht nur mit einem Würfel, sondern mit zweien, einem roten und einem blauen, würfeln, wäre der Grundraum entsprechend komplizierter. Er bestünde aus allen Paaren aus den Zahlen eins bis sechs: G={1,...,6}²={(x,y) | x,y{1,...,6}} . Bei fairen Würfeln sollte jedes Paar - also jedes Elementarereignis - gleich wahrscheinlich sein. Bei 36 Paaren ergibt sich also eine Wahrscheinlichkeit von ⁽¹⁾/₍₃₆₎

Wählt man als Attribut oder Zufallsvariable A_r:G->{1,...,6} die Augenzahl des roten Würfels und als A_b:G->{1,...,6} die des blauen, ergibt sich z. B. als Wahrscheinlichkeit für das Ereignis "der rote Würfel zeigt eine Eins" mit p(A_r=1)=p(_i=1⁶((A_r=1)(A_b=i)))=_i=1⁶p((A_r=1)(A_b=i))=⁽⁶⁾/₍₃₆₎=⁽¹⁾/₍₆₎ , wie erwartet die Wahrscheinlichkeit, mit einem Würfel eine Eins zu werfen. In diesem Fall verteilen sich die Wahrscheinlichkeiten der Augenzahlen des blauen Würfels gleichmäßig auf die Paare mit einer "roten Eins". Die Wahrscheinlichkeit jedes Paares ergibt sich so als ein Sechstel der Wahrscheinlichkeit der "roten Eins" also als ⁽¹⁾/₍₆₎·⁽¹⁾/₍₆₎=⁽¹⁾/₍₃₆₎ . Umgekehrt ist die Wahrscheinlichkeit jedes einzelnen Paares unter den Paaren mit einer "roten Eins" gerade ⁽¹⁾/₍₆₎ .

Diese Sachverhalte lassen sich folgendermaßen verallgemeinern:

4.2.1.3: Bedingte Wahrscheinlichkeit und Unabhängigkeit

Für unabhängige Ergeignisse X,YG gilt:

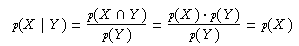
Die bedingte Wahrscheinlichkeit ist also gerade gleich der normalen Wahrscheinlichkeit. D. h. die Wahrscheinlichkeit von X wird dadurch, dass das Auftreten des Ereignisses Y zur Bedingung gemacht wird, nicht beeinflusst.

Weiter ergibt sich aus der Definiton der bedingten Wahrscheinlichkeit

p(X | Y)·p(Y)=p(XY)
p(Y | X)·p(X)=p(YX)

p(X | Y)·p(Y)=p(Y | X)·p(X)
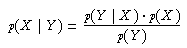