R. Ferber: Informationssysteme 1.5.2.2

4.2.2: Abschätzung des Retrievalstatuswerts nach Fuhr

Die Produktformel für die Wahrscheinlichkeit unabhängiger Ereignisse und die Bayes'sche Formel werden im folgenden verwendet, um mit vereinfachenden Annahmen die gesuchte Wahrscheinlichkeit für die Beurteilung der Relevanz eines Dokuments herzuleiten. Sie kann jetzt als bedingte Wahrscheinlichkeit geschrieben werden. Dazu verwendet Fuhr (1995 [->]) das Ereignis R "Ein Dokument wird als relevant eingeschätzt" und schreibt P(R | q,d) , also die bedingte Wahrscheinlichkeit dafür, dass eine Relevanz angegeben wird, unter der Bedingung, dass die Anfrage q und das Dokument d vorliegen.

Der zugrundeliegende Grundraum ist das kartesische Produkt G=D×Q×{R,NR} , wobei Q die Menge aller Anfragen und R bzw. NR die Beurteilung als relevant bzw. nicht relevant bedeuten. Die Schreibweise der Bedingung mit einem Komma entspricht dem Durchschnitt der Mengen, die durch geeignet definierte Attribute mit diesen Werten beschrieben werden können. Sei A_r:G->{R,NR} das Attribut, das angibt, ob ein Element aus dem Grundraum als relevant beurteilt wurde oder nicht, und A_q:G->Q das Attribut, das die verwendete Anfrage beschreibt, dann ist die Bedingung R,q=((A_r=R)(A_q=q)) , also die Menge der Elementarereignisse, bei denen ein Dokument für die Anfrage q als relevant beurteilt wurde.

Um die bedingte Wahrscheinlichkeit P(R | q,d) abschätzen zu können, geht man zunächst zu einfacheren Repräsentationen von Dokument und Anfrage über. Dazu sei T={t₁,...,t_N} die Menge der Terme, die in einer Dokumentsammlung D vorkommen. Eine Anfrage qT wird als die Menge von Termen dargestellt und ein Dokument d ebenfalls als dT oder als Vektor von Attributen bzw. Zufallsvariablen A₁,...,A_N mit

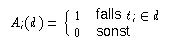
Die Vektorschreibweise besagt, dass die durch die Bedingung an die einzelnen Attribute beschriebenen Mengen konjunktiv verknüpft werden, d.h. alle erfüllt sein müssen. Um ein einzelnes Dokument zu beschreiben, kann abkürzend auch nur der Vektor mit den Bedingungswerten angegeben werden. Dieses Dokument wird dann durch d&ar;=(d₁,...,d_N){0,1}^N bezeichnet.

Eine weitere Darstellungsmöglichkeit für die Chance, dass ein Ereignis auftritt, ist der Quotient der Wahrscheinlichkeit mit der Wahrscheinlichkeit des Komplementärereignisses, die Quote des Ereignisses ( Odds).

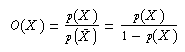
Die Quote ist <1 für Wahrscheinlichkeiten <0.5 und >1 für Wahrscheinlichkeiten >0.5 . Sie ist streng monoton, liefert also dieselbe Rangfolge für Ereignisse wie die Wahrscheinlichkeit. Sie erlaubt aber manchmal einfacheres Rechnen.

Statt der gesuchten bedingten Wahrscheinlichkeit des gesuchten Ereignisses "Es wird ein positives Relevanzurteil unter der Bedingung des Dokuments d und der Anfrage q abgegeben", wird nun ihre Quote

abgeschätzt.

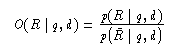
Zunächst folgt mit p(d | Rq)=^(p(dRq))/_(p(Rq)) und damit p(Rq)·p(d | Rq)=p(Rdq)

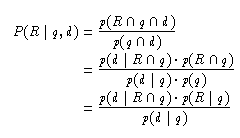
Es folgt also

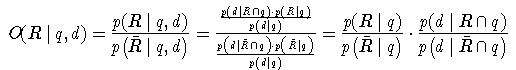
p(d | R,q) ist die bedingte Wahrscheinlichkeit eines Dokuments d unter der Bedingung, dass es zur Anfrage q als relevant beurteilt wird.

Um diese Wahrscheinlichkeit zu schätzen, müssten zu allen Anfragen Dokumente mit Relevanzbeurteilungen vorliegen. Da dieser Aufwand selten zu leisten ist, wird die Berechnung im nächsten Schritt auf die Terme heruntergebrochen. Dazu wird die starke (und unrealistische) Annahme gemacht, dass das Auftreten von Termen in Dokumenten unabhängig ist. So ergibt sich (mit I={1,...,N} )

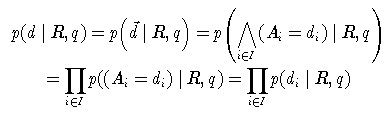
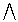
wobei _{_iI}(A_i=d_i) die konjunktive Verknüpfung der Bedingungen (A_i=d_i) an alle iI bezeichnet.

Für die Quote gilt dann:

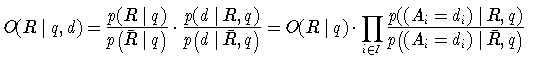
Man kann die Annahme etwas abschwächen, indem man direkt annimmt, dass

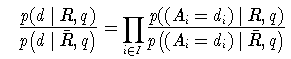
(die sog. linked dependency assumption) gilt. Allerdings ist diese Annahme wesentlich schwieriger zu interpretieren.

Zur weiteren Vereinfachung wird angenommen, dass für alle t_iT\q gilt, dass p(A_i=d_i | R,q)=p(A_i=d_i | R^-,q) ist; d. h. man nimmt an, dass für alle Terme, die nicht in der Anfrage genannt werden, die Wahrscheinlichkeit, dass sie in einem relevanten Dokument auftreten, genauso groß ist wie die, dass sie in einem nicht relevanten Dokument auftreten. Um diese vereinfachende Annahme auszunutzen, spaltet man das Produkt auf:

Der letzte Faktor dieses Produkts ist aufgrund der vereinfachenden Annahme gleich Eins, kann also weggelassen werden. Setzt man r_i=p(A_i=1 | R,q) und n_i=p(A_i=1 | R^-,q) , so kann man schreiben

da A_i ja genau dann gleich 1 ist, wenn der Term t_i im Dokument d vorkommt und sonst 0 . Da im ersten Produkt der Formel die Terme zusammengefasst sind, die im Dokument d vorkommen und im zweiten die, die nicht vorkommen, kann dort zur komplementären Wahrscheinlichkeit p(A_i=0 | R,q)=1-r_i bzw. p(A_i=0 | R^-,q)=1-n_i übergegangen werden.

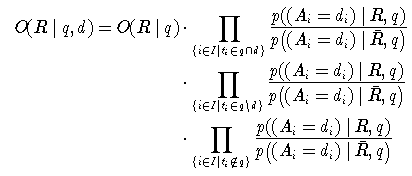
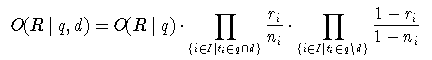
Meistens geht es darum, verschiedene Dokumente in eine Rangfolge bezüglich einer Anfrage zu bringen. Es interessieren also vor allem solche Faktoren des Produktes, die sich bei verschiedenen Dokumenten ändern. Um diese zu isolieren, kann man folgende Umformung vornehmen

Berechnet man die Werte für mehrere Dokumente d , so ist lediglich der mittlere Faktor dieses Produkts noch von den verwendeten Dokumenten abhängig, also für die Bildung einer Rangfolge relevant. Zur einfacheren Berechnung kann man auf diesen Faktor noch einen Logarithmus anwenden, der als streng monotone Funktion ja die Rangfolge nicht verändert. So erhält man als Kenngröße eines Dokuments d den Retrievalstatuswert ( retrieval status value):

Um das Verfahren anzuwenden, müssen Werte für r_i und n_i geschätzt werden. r_i ist die Wahrscheinlichkeit, dass der Term t_i in einem für die Anfrage q relevanten Dokument vorkommt, und n_i ist die Wahrscheinlichkeit, dass der Term t_i in einem für die Anfrage q nicht relevanten Dokument vorkommt.

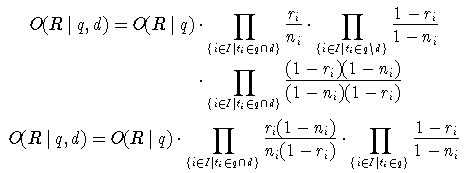
Um die Werte zu schätzen, kann eine Menge von Dokumenten verwendet werden, für die bekannt ist, ob sie für eine Anfrage relevant sind oder nicht. Diese Information kann z. B. durch Relevance Feedback Methoden ermittelt werden, also durch die Einschätzung der Relevanz der gefundenen Dokumente durch die Nutzenden. . Als Schätzung für r_i kann man die Anzahl rel_i der relevanten Dokumente, die den Term t_i enthalten, durch die Gesamtzahl rel der relevanten Dokumente teilen:

r_i~=^(rel_i)/_(rel)

Als Schätzung für n_i kann man die Anzahl nrel_i der Dokumente, die nicht als relevant eingeschätzt wurden und den Term t_i enthalten durch die Gesamtzahl nrel der nichtrelevanten Dokumente teilen

n_i~=^(nrel_i)/_(nrel)

Bei dieser Schätzung ergeben sich besonders bei kleinen Dokumentmengen Probleme, wenn eine der relativen Häufigkeiten Eins oder Null ist. In diesen Fällen ist entwerder der Bruch oder der Logarithmus nicht definiert. Ist das nicht der Fall, ergibt sich für den Retrievalstatus der Schätzwert:

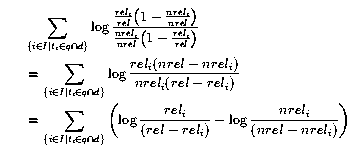
d. h. ein Term t_i trägt positiv zu der Summe bei, wenn seine Quote, berechnet mit der relativen Häufigkeit, in relevanten Dokumenten größer ist als in nicht relevanten Dokumenten. Weiter folgt, dass ein neues Dokument, das viele Terme enthält, die überproportional häufig in relevanten Dokumenten aufgetreten sind, einen hohen Statuswert erhält.

Abb. 40: Beispiele mit Relevanzangaben zur Schätzung des Retrievalstatuswertes zu einer Anfrage q=t1,...,t6

Abb. 41: Neue Dokumente und ihr Retrievalstatuswert

Bei diesem Verfahren muß zu jeder Anfrage zunächst eine Menge von Dokumenten auf ihre Relevanz bezüglich der Anfrage beurteilt werden, damit anschließend zusätzliche Dokumente bewertet werden können. Das ist immer noch ein aufwendiges Verfahren.

Eine Möglichkeit dieses Verfahren zu verallgemeinern besteht darin, über verschiedene Anfragen zu mitteln, d. h. solche Terme hoch zu gewichten, die in vielen Dokumenten viel zu der Summe des Statuswertes beitragen.