



 |
 |
 |
 |
Um die Konsistenzprobleme, die sich bei einer strengen logischen Interpretation ergeben anzugehen, kann man eine probabilistische Inferenz einführen. Sie schätzt die Wahrscheinlichkeit p(d->q) , dass eine Folgerung gilt - hier: dass die Anfrage q aus dem Dokument d gefolgert werden kann - , ab. Dazu kann man zunächst jedes Dokument als eine " mögliche Welt" ( possible World) betrachten, also als eine Menge von Aussagen mit zugehörigen Wahrheitswerten. Das Prinzip der unsicheren oder probabilistischen Inferenz ist nun folgendes: Es seien zwei Aussagen x und y gegeben. Als Maß der Unsicherheit der Aussage y->x bezüglich einer gegebenen Datenbasis kann der Umfang der kleinsten Informationsmenge gewählt werden, die zu der Datenbasis hinzugefügt werden muss, damit die Aussage y->x gültig ist.
Aus dieser eher vagen
Beschreibung leitet van
Rijsbergen schrittweise konkreter werdend
einen Algorithums ab, mit dem Dokumente in eine Rangfolge
bezüglich einer Anfrage gebracht werden können.
Dazu benötigt man eine
Ähnlichkeitsfunktion zwischen
den "möglichen Welten"
w W und
eine
Wahrscheinlichkeitsfunktion p auf dem Grundraum
W .
W und
eine
Wahrscheinlichkeitsfunktion p auf dem Grundraum
W .
Im Laufe dieser Ableitung wird sich zeigen, dass sich das System dabei im wesentlichen auf ein gewichtetes Vektorraummodell reduziert, bei dem aus dem Korpus gewonnene Ähnlichkeiten zwischen Termen bei der Gewichtung berücksichtigt werden.
Seien nun wieder
x und y zwei Aussagen und w W eine "mögliche Welt".
Mit
W eine "mögliche Welt".
Mit
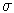 (w,y)
(w,y)
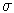 (w,y) gilt. Bezeichne
(w,y) gilt. Bezeichne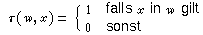
 (w,y->x)=
(w,y->x)= (
(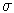 (w,y),x)
(w,y),x)
Die Wahrscheinlichkeit p(y->x) wird nun folgendermaßen definiert:
 w
w Wp(w)
Wp(w) (w,y->x)=
(w,y->x)= w
w Wp(w)
Wp(w) (
(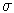 (w,y),x)
(w,y),x)
Man kann die Imagingtechnik auf Dokumente als "mögliche Welten" anwenden. Dabei ergibt sich aber das Problem, dass auch die Aussage y ein Dokument ist. Nimmt man an, dass ein Dokument in einem anderen Dokument nur dann "gültig" ist, wenn es eine Teilmenge des letzteren ist, könnten beim Imaging nur solche Dokumente verwendet werden, bei denen das eine im anderen enthalten ist. Solche Dokumente sind aber vermutlich selten.
Crestani und van Rijsbergen (1995 [->]) wählen deshalb eine Menge T von Termen als "mögliche Welten". Die Wahrscheinlichkeit der Inferenz von einem Dokument d auf eine Anfrage q ergibt sich dann als
 t
t Tp(t)
Tp(t) (
(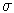 (t,d),q)
(t,d),q)
Inhaltlich kann ein Term im einfachsten Fall als durch die Menge der Dokumente repräsentiert angesehen werden, in denen er auftritt. D. h. ein Dokument bzw. eine Anfrage ist in einem Term "gültig", wenn der Term darin auftaucht. Hat man zusätzlich eine Ähnlichkeitsfunktion zwischen Termen, so wird beim Imaging die Wahrscheinlichkeit eines Terms, der nicht in einem Dokument auftaucht, auf den nächstgelegenen Term aus dem Dokument übertragen.
Die globale Wahrscheinlichkeit p(d->q) für ein Dokument d T und eine Anfrage q
T und eine Anfrage q T kann folgendermaßen berechnet werden:
T kann folgendermaßen berechnet werden:
 T\d der Term t'
T\d der Term t' d bestimmt, der t am ähnlichsten ist.
d bestimmt, der t am ähnlichsten ist. Abb. 43: Imaging
Abb. 43: ImagingEntscheidend für diese Bewertung sind die Wahrscheinlichkeiten der Terme und das Ähnlichkeitsmaß zwischen den Termen. Da sie lediglich an einer Rangordnung der Dokumente interessiert sind, wählen Crestani und van Rijsbergen (1995 [->]) anstelle einer Wahrscheinlichkeit das IDF-Maß
Als Ähnlichkeitsmaß wählen Crestani und van Rijsbergen das EMIM Maß:
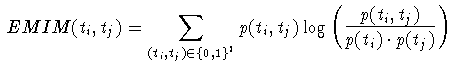
Mit den Daten aus der Cranfield Collection wurden Versuche gemacht, wobei zwei Läufe verglichen wurden, einer mit Imaging und einer, in dem lediglich die IDF Werte als Gewichtungen verwendet wurden. Die Ergebnisse zeigen leicht bessere Ergebnisse für Imaging. Der Unterschied ist aber statistisch nicht signifikant.
 Abb. 44: Probleme des Imaging
Abb. 44: Probleme des Imaging |
 |
 |
 |