



 |
 |
 |
 |
Während in Clusterverfahren Teilmengen von ähnlichen Beispielen konstruiert werden, kann man auch versuchen, die Definition von Mengen so zu verallgemeinern, dass vage Zuordnungen von Beispielen in unterschiedliche Teilmengen besser abgebildet werden können. Dazu wurden bereits 1965 von L. A. Zadeh [->] sogenannte unscharfe Mengen oder Fuzzy Sets eingeführt. Die folgende Darstellung orientiert sich an Bademer & Gottwald [->] (1993).
Die Theorie der Fuzzy Sets stellt als eine Verallgemeinerung des Mengenkonzepts den "Grad der Mitgliedschaft in einer Menge" zur Verfügung. Diese Verallgemeinerung wird mit Hilfe einer Zugehörigkeitsfunktion definiert:
 4.5.2.1: Fuzzy Set
4.5.2.1: Fuzzy SetBei unscharfen Mengen muss für ein Element also nicht mehr eindeutig gesagt oder bestimmt werden, ob es in einer bestimmten Menge liegt oder nicht, sondern es kann ein Zahlenwert zwischen Null und Eins angegeben werden, der die Zugehörigkeit des Elements zu der Menge beschreibt. Das entspricht der Gewichtung von Termen in der Vektordarstellung eines Dokuments. Dort war allerdings keine Einschränkung der Werte auf das Intervall [0,1] festgelegt worden. Eine solche Einschränkung kann allerdings im Allgemeinen durch eine geeignete Normierung erreicht werden. Dabei müssen aber die Auswirkungen auf die verwendeten Ähnlichkeitsmaße berücksichtigt werden. Andererseits ist die Definition von unscharfen Mengen nicht auf eine endliche Menge von Termen beschränkt. Sie wurde für beliebige Mengen eingeführt.
Die herkömmliche Mengendefinition (oder die Definition einer
scharfen Menge) läßt sich als Spezialfall der Definition
einer unscharfen Menge schreiben. Dazu wählt man als
Zugehörigkeitsfunktion einer Menge U D die charakteristische
Funktion:
D die charakteristische
Funktion:
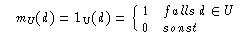
Das ist das gleiche Vorgehen, wie bei der Beschreibung des Booleschen Retrievals als Spezialfall des Vektorraummodells.
 Abb. 62: Unscharfe Mengen als Beschreibung von Lebensaltern
Abb. 62: Unscharfe Mengen als Beschreibung von LebensalternZwei unscharfe Mengen sind genau dann gleich, wenn ihre Zugehörigkeitsfunktionen gleich sind. Die leere unscharfe Menge ist durch die Zugehörigkeitsfunktion
 0
0
 1
1
 4.5.2.2: Träger, Kern, Schnitte und Höhe
4.5.2.2: Träger, Kern, Schnitte und HöheZur weiteren Untersuchung der Eigenschaften unscharfer Mengen, bzw. zur weiteren Verallgemeinerung von Eigenschaften scharfer Mengen auf unscharfe Mengen kann man die folgende Aussage benutzen, die eine Beziehung zwischen scharfen und unscharfen Mengen herstellt.
 4.5.2.3: Aussage:
4.5.2.3: Aussage: Abb. 63: Rekonstruktion des Wertes der Zugehörigkeitsfunktion aus einem
Abb. 63: Rekonstruktion des Wertes der Zugehörigkeitsfunktion aus einem Mit dieser Äquivalenz lassen sich Eigenschaften und
Operationen von scharfen Mengen auf unscharfe Mengen übertragen.
Geht man von der Teilmengenrelation für scharfe Mengen aus, kann
man fordern, dass die 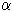 - Schnitte einer Teilmengenrelation unscharfer
Mengen die Teilmengenrelation für scharfe Schnitte erfüllen
sollen. Man erhält als Definition also
- Schnitte einer Teilmengenrelation unscharfer
Mengen die Teilmengenrelation für scharfe Schnitte erfüllen
sollen. Man erhält als Definition also
 X:
X: Y>=
Y>=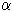
 X>=
X>=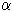

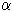
 [0,1]
[0,1]
Aus der rechten Seite kann man eine äquivalente Bedingung
für die Zugehörigkeitsfunktionen ableiten: Für ein
beliebiges d D setzen wir
D setzen wir 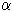 =mY(d) . Dann folgt aus d
=mY(d) . Dann folgt aus d Y>=
Y>=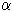 dass auch d
dass auch d X>=
X>=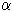 gilt und damit mX(d)>=
gilt und damit mX(d)>=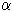 also mX(d)>=mY(d)
also mX(d)>=mY(d)  d
d D .
D .
Umgekehrt folgt aus mX(d)>=mY(d)  d
d D nach der Definition des Schnittes X>=
D nach der Definition des Schnittes X>=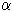
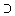 Y>=
Y>=
Zusammen gilt also
 X
X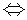 mY(d)<=mX(d)
mY(d)<=mX(d)  d
d D
D
Man kann also für unscharfe Mengen die Teilmengenrelation durch diese Äquivalenz definieren.
Es folgt dann unmittelbar für diese Teilmengenrelation:
 X
X D
D
 X, X
X, X Y
Y Y=X
Y=X
 X, X
X, X W
W  Y
Y W
W
Wie bei den scharfen Mengen gibt es auch bei unscharfen Mengen verschiedene sinnvolle Maße für die Größe einer Menge, je nachdem ob der Träger endlich, abzählbar oder meßbar ist. Bei endlichem Träger kann man analog zur Anzahl der Elemente einer scharfen Menge die Summe der Werte der Zugehörigkeitsfunktion verwenden.
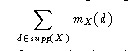
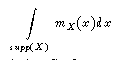
 4.5.2.4: Vereinigung, Durchschnitt und Komplement
4.5.2.4: Vereinigung, Durchschnitt und Komplement Abb. 64: Vereinigung und Durchschnitt von unscharfen Mengen
Abb. 64: Vereinigung und Durchschnitt von unscharfen MengenMan sieht, dass sich diese Definitionen bei der Verwendung von scharfen Mengen, also von charakteristischen Funktionen, mit den herkömmlichen Definitionen von Vereinigung, Durchschnitt und Komplement decken.
Aus den entsprechenden Eigenschaften der Maximumsfunktion ergeben sich auch sofort
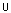 X=X
X=X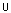 Y
Y
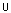 X)
X)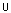 W=X
W=X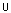 (Y
(Y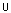 W)
W)
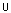 X=X
X=X
 X
X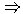 Y
Y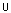 W
W X
X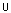 W
W
Diese Eigenschaften lassen sich auch für den Durchschnitt zeigen. Entsprechend lassen sich auch Distributivgesetzte und deMorgansche Regeln auf unscharfe Mengen übertragen. Schließlich gilt
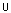 X)>
X)>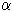 =Y>
=Y>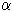
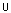 X>
X>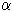
 X)>
X)>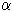 =Y>
=Y>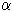
 X>
X>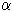
Neben dieser "kanonischen" Definition von Vereinigung und Durchschnittsbildung gibt es noch weitere Möglichkeiten, solche Operationen zu definieren. Darauf soll hier aber nicht eingegangen werden.
Es soll im folgenden aber noch angedeutet werden, wie Fuzzy Methoden zum unscharfen Schließen bzw. unscharfen Kategorisieren verwendet werden können. Dazu kann man unscharfe Relationen analog zu scharfen Relationen als Teilmengen der entsprechenden kartesischen Produkte definieren:
Eine (scharfe) Relation zwischen zwei Attributen A1:D->R1 und A2:D->R2 kann als Teilmenge des kartesischen Produkts der Wertemenge der Attribute geschrieben werden.
 R1×R2={(x,y) | x
R1×R2={(x,y) | x R1,y
R1,y R2}
R2}
Die Gleichheit zweier Attribute kann damit z. B. als Relation der Form
Kategorisierungsregeln, wie sie z. B. beim AQ-Algorithmus beschrieben wurden, können auch als Relationen dargestellt werden. Im folgenden beschränken wir uns der Einfachheit halber auf Kategorisierungen, die durch ein vorherzusagendes Attribut A2 beschrieben sind, und sich nur auf ein vorhersagendes Attribut A1 stützen. Wie beschrieben, läßt sich ja jede Kategorisierung durch die geeignete Wahl bzw. Konstruktion von A1 auf diese Aufgabe reduzieren. Sie ist dann eine Funktion, die sich als Regel in der Form
IF (A1=x)
THEN
A2=y
schreiben lässt und als Relation in der Form
Die charakteristische Funktion der Gleichheitsrelation auf der Menge der Paare ergibt sich z. B. für R=R1=R2={0,1,2} in der Form:
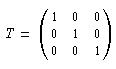
 R als x=(0,1,0)t , so ergibt sich die Kategorisierung als
Multiplikation der Matrix T mit dem Vektor x . Man kann sie in der Form
R als x=(0,1,0)t , so ergibt sich die Kategorisierung als
Multiplikation der Matrix T mit dem Vektor x . Man kann sie in der Form
IF (A1=x)
THEN
A2=T·x
schreiben oder einfacher als
In dieser Weise werden Kategorisierungen beschrieben, solange die Matrix eine Permutationsmatrix ist, d. h. solange in jeder Zeile und in jeder Spalte genau eine 1 steht. Allgemeiner kann man die IF-THEN Regel als eine Verknüpfung der charakteristischen Funktion des Wertes von A1 mit der Relation betrachten.
Die Darstellung der Relation durch die charakteristische Funktion ermöglicht die Verallgemeinerung der Relation zu einer unscharfen Relation und damit die Definition einer unscharfen Kategorisierung. Während bei der scharfen Relation nur 0 und 1 als Beschreibungen der Zugehörigkeit zulässig sind, sind bei der unscharfen Relation Zugehörigkeiten aus dem Intervall [0,1] erlaubt, z. B:
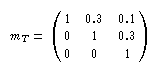
Eine unscharfe IF-THEN-Regel kann nun mit Hilfe einer unscharfen Relation folgendermaßen geschrieben werden:
IF (A1=X)
THEN
A2=Y
wobei X und Y unscharfe Mengen sind und die Zugehörigkeitsfunktion von Y folgendermaßen definiert ist:
 R1
R1 y
y R2
R2
 |
 |
 |
 |