3.1.3: Das P-Norm-Modell
Schließlich beschreiben Fox, Betrabet, Koushik und Lee (1992)
[->]
noch
das P-Norm-Modell. Hier sind
auch im Anfragevektor
Einträge zwischen 0 und 1 zugelassen.
Als Ähnlichkeitsmaß für eine OR-Anfrage wird die Formel
|
| s(wi,q)=1- |
| ( |
| n |
 |
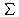| j=1 |
| ((1-wi,j)qj)p |
)1/p |
|
 |
| ( |
| n |
|
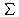| j=1 |
| qpj |
)1/p |
|
|
mit
p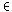 {1,...,∞}
verwendet.
Für p=1
und Anfragevektoren, die nur aus
den Werten 0 und 1 bestehen, handelt es sich also um die
gleiche Formel (128
) wie bei
der Paice-Ähnlichkeit mit c=1
.
Für größere Werte von p
beschreibt der
Zähler die P-Norm-Länge der Projektion des Dokumentvektors auf den Unterraum, der von
den Anfragetermen aufgespannt wird, für p=2
also die euklidische Länge dieses Vektors.
Dieser Wert wird mit der p-Norm-Länge des
Anfragevektors normiert. Falls im Anfragevektor auch Werte
zwischen 0 und 1 zugelassen sind, wird der Unterraum entsprechend
afin abgebildet, d.h., die Skalen seiner Achsen werden
verändert.
Fox, Betrabet, Koushik und Lee (1992) [->]
geben als
Heuristik für die Wahl des Maßes den Abstand zum Ursprung des Unterraums an.
Als Ähnlichkeitsmaß für eine AND-Anfrage
wählen sie die Formel
| s |
(wi,q) |
=1- |
| ( |
| n |
|
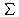| j=1 |
| (
(1-wi,j)qj
)p |
)1/p |
|
|
| ( |
| n |
|
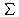| j=1 |
| qpj |
)1/p |
|
|
mit
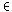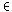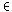p{1,...,∞}
und interpretieren diesen Wert als Abstand der
Projektion des Dokumentvektors vom Punkt
(1,...,1)
im Unterraum, der von den Termen der
Anfrage aufgespannt wird.
|
